A cura di Stefano Fait
Web Caffè Bookique [Facebook]
A Superconducting Model
of the Sun
by Bernard Burchell
There are two popular and competing models that describe how the Sun works. As in, how it glows, gives off heat, light, solar wind, etc.
The most well-known of these is the thermonuclear model.
In this model, loose accumulations of interstellar hydrogen are drawn together under the pull of their own gravity and into a sphere of compressing gas. The process involves friction, which causes the gas to glow either red or infrared, and leads to what we call a brown dwarf.
If this process were allowed to continue, and with increasingly larger amounts of hydrogen involved, the pressure at the interior of the ball would become so high that the hydrogen would undergo nuclear fusion: first into helium, and then into higher order elements. The energy released by this fusion process would cause the gaseous ball to glow white-hot, leading to a star like our Sun.
In the thermonuclear model the Sun’s interior is millions of degrees Celsius. This steadily decreases toward the surface where we observe a temperature of around five thousand degrees.
A lesser-known explanation is the electric model.
In this model, the glow we observe from the Sun’s surface is not caused by fusion but by electrical discharges; similar to the electric arcs/sparks seen on a welding device. For this to happen the Sun must have a strong net-positive charge. It is made out of plasma (ionised gas) and this positive plasma steadily discharges at its surface. Its interior is a few thousand degrees throughout; slightly cooler than the photosphere surface. And its interior charge counteracts gravity to prevent further collapse.
(The above is a very brief introduction and admittedly the subject takes some getting used to. For a better description of the Electric Sun model see
http://www.electric-cosmos.org/sun.htm )
http://www.youtube.com/playlist?list=PLwOAYhBuU3Ufr53AnJv9RLousgVN4G_uX
Of these two models, the more likely is the electrical one. It correctly accounts for the magnetic fields, the appearance of tufts, its temperature increase whilst heading outward toward the corona, the solar wind, and occasional flaring.

In these close-ups of sunspots we see twisted glowing strands. These are consistent with Birkeland currents, a type of electrical arcing seen in plasma discharges. Credit: SST, Royal Swedish Acadmey of Sciences

Here we see coronial plasma loops, an effect related to magnetism. The Sun’s magnetic field can also be detected far out into the solar system. Credit: M. Aschwanden et al. (LMSAL), TRACE, NASA
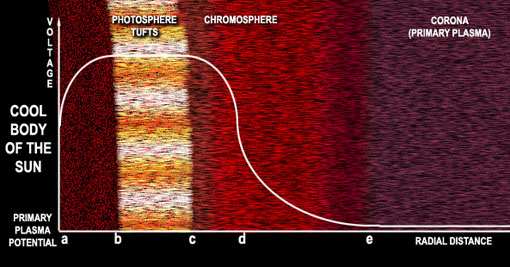
This diagram shows the Sun as a large positively charged ball and the voltage potential arising from it. The high positive charge causes a discharge of protons into the photospheric gasses, leading to plasma glowing effects. The protons then continue to accelerate and strike the corona (an outer layer of gas surrounding the Sun) at high speed, leading to even higher temperatures there. Credit: The Electric Universe, Thornhill & Talbott
Where’s the power?
Despite its success though, the electric Sun model does appear to suffer a major deficiency. Namely the question: what powers this electrical giant? Specifically, what gives it a positive charge, and what drives the currents necessary to explain its magnetic fields?
According to the theory, the Sun is powered by streams of electrons funnelling inward toward the polar regions. These ‘galactic powerlines’ interconnect all the stars in the galaxy and feed them the necessary current to power their photospheres. The presence of these has been partially observed via the Ulysses craft, which passed over the polar regions [1].
But while there could be little disagreement that a positively-charged ball would attract electrons, there are major problems in suggesting that this could be its power source.
First, a stream of electrons ‘falling’ into the Sun is not going to do much other than steadily discharge it. In order to power an electrical device (e.g. a desk lamp), charge must be forcefully fed into it and then extracted again. This is because the device has resistance that needs to be overcome. But the electrical Sun model describes a one-way inward current flow. And it’s not forced, just free-falling.
Second, since the Sun is emitting positive charges, the net current supply must consist of protons rather than electrons otherwise the output current – the solar wind – would eventually cease. This is a big problem because protons won’t move toward a net-positive charge unless they are somehow forced or initially fired (from where?) at high speeds. But the model allows for no such inward positive flow and no observations support it.
So what then could explain the power supply and nature of the Sun?
What if…?
What if, instead of the high-temperature thermonuclear model, we said the Sun steadily grew cooler as we headed inwards? And by ‘cooler’, I don’t just mean in a sense relative to its surface, as in a few thousand degrees. Nor even a few hundred degrees. And not even a few degrees below room temperature, but colder again.
What if the temperatures in the Sun’s interior became so cold that they approached levels nearing absolute zero Kelvin – the lowest temperature possible for any material?
The idea sounds absurd! It is the complete opposite of the conventional model, with its millions-of-degrees thermonuclear core. And after all,how could a compressed gas become cold?
Extreme compression of a gas
To understand how this might be possible, consider an airtight cylinder with a piston at one end. We fill the cylinder with nitrogen (which is basically air minus oxygen) and begin to apply pressure to the piston. What will happen?
This is somewhat like compressing air inside a bicycle pump. The pressure will increase and the temperature will rise. After a while though, this heat from the compression process will dissipate and the temperature will return to the surrounding air temperature.
So we push the piston further. Once again, the nitrogen pressure will increase and the temperature will temporarily rise before returning to normal.
Now let’s suppose our cylinder was very strong and we were able to apply a very high amount of force to the piston. In this case the gas will compress so much that it will cease being a gas and become a liquid: liquid nitrogen.
Take this idea further. We continue to apply ever larger forces on the piston. Eventually this liquid will be forced to collapse into ‘solidnitrogen’.
As is well known, liquid and solid nitrogen are very cold substances. However it needs to be quickly pointed out that we have not made anything cold. Rather, the liquid and solid states of nitrogen will at first be at high temperature and pressure. After a while, the heat will dissipate and temperature will return to the surrounding air temperature. But compared to regular (cold) liquid or solid nitrogen, the pressure is very high and the substance would explode into gas if released.
Compression under gravity
Now consider a similar situation for a star. Under the standard astronomy model, stars are formed when loose accumulations of hydrogen gas are drawn together under the force of their own gravity. As this occurs, gas is compressed and heats up, giving out infrared heat. This increase in temperature might halt the compression process for a time. But adding more gas will force the compression to continue.
Eventually the internal gaseous resistance will give way, allowing the hydrogen to liquefy. Although this liquid will be still be quite hot. We continue to add more hydrogen, increasing the external pressure. Eventually this liquid also gives way, and the hydrogen collapses into a solid.
At this stage the solid is somewhat disorganised, its atoms not arranged according to any particular pattern. We continue to increase pressure. Eventually the hydrogen atoms are forced into crystalline lattice structures. We could now refer to this as ‘metallic hydrogen’.
The atoms have now become rather restricted in their movement. They are unable to move about freely as they did in their gas, liquid or semi-solid state. Instead they are restricted into vibrating along short distances.
Despite the restriction in distance though, this rapid movement still accounts for a high temperature; since that vibration is essentially the definition of temperature. But if enough pressure were applied to the lattice, the hydrogen atoms would be almost unable to move. They would effectively have become frozen and could thus be described as having a temperature of near absolute zero.
So… what happens when we freeze a metal or crystalline material to near absolute zero? The title of this essay gives it away: it becomes superconducting!
As is known, superconductors allow electrons to flow through them without resistance. A superconductor formed into a ring or disk can maintain an internal electric current that circles forever. And as it does so, it emits a magnetic field, just as an electromagnetic coil would do. Except a superconductor magnet requires no power supply to maintain it.
Therefore a superconductor formed into a ball should also be able to maintain internal currents that cycled forever and without the need for any power supply.
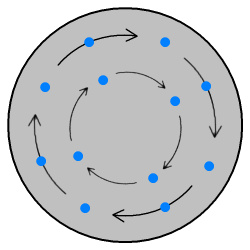
Electrons circling within a superconducting ball or disk.
Current cross-section of a wire
So what does this mean? Quite obviously, if the Sun were a giant superconductor, we should likewise expect it to contain powerful circling currents. These currents would then generate large magnetic fields. And we certainly do observe magnetic fields and related effects like plasma loops coming from the Sun (see eariler diagram).
But there is more to this story than just magnetism.
Consider now two parallel wires, each carrying a current in the same direction. We know from observation that these will attract each other.
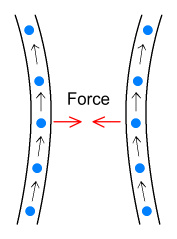
Magnetic attraction from parallel currents.
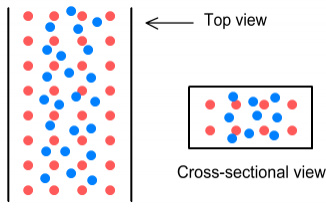
Now consider the situation inside just a single current-carrying wire. We will give this wire a rectangular cross section, with width is twice its depth. Below is an enlarged top and cross-section view.
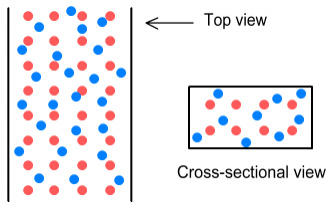
Electrons stationary inside a wire with rectangular cross-section.
Here we see the wire with protons and electrons both stationary, i.e. no current is flowing yet. If we draw an imaginary dividing line down the middle of the wire we notice that it would become analogous to the two parallel current-carrying wires described earlier, except without a gap between them. Therefore, like the two-wire situation, we should expect flowing electron streams to attract each other like so:
Electrons flowing inside a wire with rectangular cross-section.
Here we see an electron current flowing and the electrons are now concentrated along the middle of the wire. This gives the inner part of the wire a slight negative charge. Meanwhile the outer edges of the wire have a lack of electrons and therefore gain a slight positive charge.
Does this happen in reality? It doesn’t. Experiments show that current density remains uniform when DC currents are involved. And when an AC current is fed through, the electrons push themselves against the walls of a wire. This is called the ‘skin effect’.
Given our knowledge of magnetism however, this appears curious. Because by all accounts the electrons should accumulate into the middle portion of the wire in both the DC and AC scenarios.
It appears something else is going on inside wires, namely ‘eddy currents’. These are tiny ‘whirlpool’ currents that appear to develop inside conductors, repelling attractive current flow and pushing the electrons to the outside. In the AC case the effect is more pronounced.
But we are not dealing with regular conductors. We are dealing with superconductors, and these have rather different properties where magnetism is concerned. Given that superconductors have zero resistance, perhaps eddy currents don’t develop or are too minor to be a problem. Therefore for superconducting wire, especially where large currents are concerned, magnetic forces may well focus the electrons along the middle of the wire, as indicated above.
Next consider the situation for a superconducting disk. We’ll start by having electrons circle around its centre.
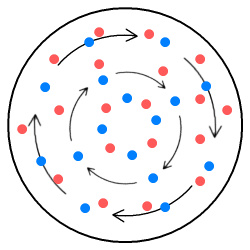
Electrons circling in disk (no magnetic attraction).
Since these electrons are moving in parallel, we should expect them to magnetically attract each other, resulting in a situation like this:
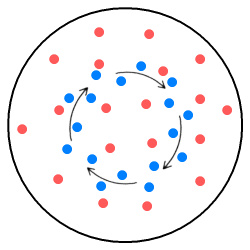
Electrons circling in disk, with internal magnetic attraction.
As with the rectangular wire above, the electrons have concentrated themselves into a negatively charged ring-shaped region located between the centre and the perimeter. The reason for a ring and not a small inner disk is that the electrons moving in opposite directions on either side of the ‘inner disk’ will magnetically repel each other. The result will be a negatively charged ring with a positively charged regions either side: one in the centre and the other along the outer part of the disk, as shown below.
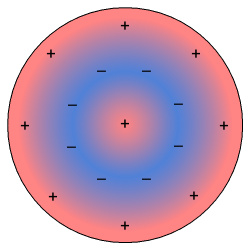
(Fig 10) Magnetic attraction and repulsion of circling electrons leaves positive and negative regions within a disk.
Now extend the above situation to a ball-shaped superconductor. Particularly one the size of the Sun. We should expect large internal currents, which focus themselves into a middle negative region, whilst leaving a positive region in the centre and on the outside.
This outer positive region is of particular interest. If the charge were strong enough, we should expect electrical discharges to occur across the surface of the Sun, as protons leapt off the surface.
If the surface were covered by a gaseous layer (and it is with the Sun) the motion of protons passing through it would cause the surface to light up with electrical sparks, also known as ‘anode tufts’. We should also expect a steady discharge of protons accelerating out as a solar wind. And if for some reason the sparking stopped at some area, causing sunspots, we should also expect those regions to be darker because we would now be looking at the relatively cooler solid surface of the Sun. And sure enough, this all corresponds to what we see!
Since currents can circle forever within a superconductor, the above describes a model in which a star can glow indefinitely, without any external power source or requirement for internal fusion. Electrons will still be attracted and flow inward toward the Sun’s positive surface. However, these are not required for the Sun to glow and act more as a power discharge than a power supply.
What about density?
In order for this model to be viable it needs to show an agreeable density. The density of the Sun is 1400kg/m3 or 1.4 times that of water. This is of course an average. We should expect the density to be less near the surface and steadily increase toward a value higher at the centre.
So how does the 1400 number fit with this model?
Below is a table showing the densities of various substances in ascending order and compared with the Sun’s average.
Substance Density (kg/m3)
Hydrogen gas 0.09
Helium gas 0.18
Helium solid 0.21
Nitrogen gas 1.3
Tungsten Hexafluoride gas 13
Hydrogen liquid 71
Helium liquid 125
Lithium solid 534
Hydrogen solid 600
Nitrogen liquid 807
Water liquid 1000
Nitrogen solid 1030
Sun (average) 1400
Quartz (SiO2 – typical rock) 2600
Diamond (carbon) 3500
Iron 7900
Lead 11000
Note the position of hydrogen gas on the list. At 0.09 kg/m3, it is far less than the 1400 required. Likewise with heavier gasses such as helium and nitrogen. In fact even the densest gas known, tungsten hexafluoride, falls well short of what is required. This would appear to rule out an interior of a gaseous or plasma nature.
Hydrogen in its liquid state is still too light, as is helium. Liquids made of heavier elements would certainly work, although that requires them to be far above hydrogen on the periodic table, and which requires going back to the problematic fusion model.
Going to typical solids, such as diamond (compressed carbon) places us too high on the list. Carbon is said to be a common fusion by-product in the thermonuclear model.
But solid hydrogen appears nearer the mark.
Solid hydrogen has a density of 600kg/m3. The 1400 Sun-density value seems to correspond to hydrogen compressed to a bit over double that amount. If we estimate a higher density for the Sun’s interior of 1800kg/m3, that makes it 3 times the 600 hydrogen figure. Admittedly the 1800 number is a guess and the real density might be higher; although could not be too much higher because the 1400 average would be wrong.
Thus, a Sun comprised of compressed solidified hydrogen would have a density consistent with what we observe, and is supportive of the model described here.
Of course it would also be possible to achieve the 1400 average using a combination of elements. Metallic lithium for example has a density of 534kg/m3. So compressing that several times can give the necessary density. Or combining it with heavier elements like iron would also work. However, it will require fusion and also require the relative abundance of such substances be very different than what is observed in the universe. Thus metallic hydrogen still seems the more likely candidate [2].
Solar Oblateness and Rotation
Here’s another point to consider. As we know, the Sun rotates on its axis, and this rotation gives rise to a bulge around its equator, similar to the way the Earth bulges around its equator.
The degree of bulge – called the solar oblateness – however, is far smaller than what would be expected for a flexible rotating ball of that size, mass and angular speed. In fact the Sun comes close to being a perfect sphere.
But if the interior of the Sun were not made of gas or plasma, and was instead a solid ball, the above observations on oblateness would make sense. Because only the outer flexible layer of the photosphere gasses would be able to bulge and the amount of bulge would be limited by its thickness.
And speaking of rotation, another interesting fact is that the Sun rotates faster at its equator than at its poles. This tells us that some of the observed rotation may just be a surface effect and leads to the possibility that the interior may be rotating even slower again. In fact for all we know, the interior may not rotate at all and the surface rotation we observe may be caused by interior electrical currents pushing the photosphere around. If this were the case it would explain why the interior solid region formed as a sphere rather than an ‘ellipsoid’.
The overall current flow
Let’s now look at the overall current flow. The above diagram (Fig 10) showing positive and negative regions within a disk won’t work for a sphere. Namely, it won’t be possible for currents to circle a sphere in all directions because electrons moving head-on would magnetically repel. Therefore, it will instead be necessary for currents to largely flow in the same direction.
In the previous section it was speculated that the Sun’s apparent rotation only represented the flow of its photosphere, and that this was being caused by the electron currents flowing in the solid interior.
This does seem likely. Since the gasses within the photosphere are ionized into a plasma, the protons within the plasma would be magnetically attracted to the circling electrons and dragged across the solid surface underneath. Meanwhile the electrons in the photosphere will move along with the protons, giving an overall movement of the photosphere surface.
This motion of the photosphere suggests an interior current flow in layers, i.e. many current loops running parallel to the Sun’s equator. The overall current flow and resulting charged regions will then look something like this:
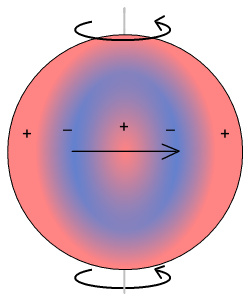
(Fig 11) Electron currents cycle eastwards along the equator and in many layers parallel to it. This leaves positive and negative regions within. Arrows represent direction of electron flow and the vertical grey line is an “axis” of rotation.
As with the disk, this results in positive and negative regions within. What happens at the polar regions is uncertain since we won’t be able to fit in a ‘mini disk’ there. So here they are speculatively shown as having the adjacent positive regions spill over onto them. As a result we end up with a sphere covered by an outer positive layer.
Magnetic repulsion of the surface
Next we’ll look at the interaction between the moving photosphere and stationary interior.
In this model, protons within the solid interior remain stationary while the electrons cycle west-to-east, and the photosphere moves in the same direction, albeit more slowly.
Since the protons in the photosphere are moving against those in the interior, they will magnetically repel and be pushed away. Meanwhile the electrons in the photosphere will be magnetically attracted. This diagram shows the resulting force directions.
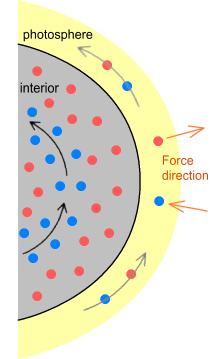
(Fig 12) Magnetic attraction/repulsion between photosphere and interior (top view, looking down on north pole). Protons experience repulsion and electrons attraction as they both move over the net-positive surface of the interior.
This interaction turns out to be very important. We know from Coulomb’s law that a sphere containing equal amounts of positive and negative charge can have zero net-attraction. This will be the case when the charge is distributed with radial symmetry, i.e. if the charge is arranged into positive and negative spherical shells. The charge distribution diagram above (Fig 11) shows something close to this situation.
But if differently charged regions of the interior and exterior regions were moving against each other (as indicated in Fig 12), this can lead to a net repulsion of the photosphere’s protons, resulting in a glow-discharge and solar winds.
In fact without the photosphere’s rotation, it might be that the Sun wouldn’t glow at all. It might also be true that sunspots are caused by a slowing down of photosphere motion (for unknown reasons), and hence a halting of the discharge process at those places.
No miniature stars
The electric star model discussed at the opening of this essay is part of a broader body of knowledge and theory known as the Electric Universe (EU) model. One of the big benefits of the EU model is that it is able to recreate observed astronomical phenomena in a laboratory. For example it is possible to produce phenomena that look strikingly similar to nebulae formations inside plasma focus devices.
The fact that we can do this is very impressive and tells us EU theory must be on the right track in much of what it describes.
Despite this validity however, no similar success has been achieved in creating a small-scale star in a laboratory. The same is true throughout the universe: no miniature stars are seen floating about our galaxy or elsewhere. It appears that white stars must be of a minimum size or they won’t function.
This should be a big clue that there is more than just electricity at play in creating a star. Namely, that a large amount of gravity is required in order for a star to advance beyond the brown dwarf stage and become a white star. This point further supports the compressed superconducting model.
How long can it last?
Can the Sun/star model described here radiate forever? On the face of it it would appear so. Superconductors can maintain a current continuously without decrease. Therefore it would seem that stars could output an unlimited supply of energy.
Problem is, our Sun also outputs solar wind and flares – amounting to a million tons of matter every second and consisting mainly of protons. This process clearly can’t continue forever. At some point it must come to a stop when the Sun runs out of ejectable protons or becomes too negatively charged (as a result of losing protons) and is unable to eject more. At this point the electrical discharges in the photosphere would cease and the Sun would become dark.
Another consideration is the inflow of electrons. As discussed earlier, a positive charged surface would be expected to attract a steady stream of electrons. Initially these electrons might add to the those already circling within the interior. This would increase the current flows, the magnetic fields, and the brightness/intensity of the solar output. Eventually though, the increase in negative charge would be enough to halt the output of protons, again leading to the Sun’s demise.
Fusion
Something also needs to be said about the conversion of hydrogen into heavier elements, i.e. fusion. The electric star model forbids fusion within the Sun’s interior but allows for it to take place within the electrical discharge area of the photosphere.
In this superconductor model we’ll allow that the same should apply. Namely that there should be no fusion activity within the frozen interior but that fusion will take place either in the photosphere or just beneath it. How long this can continue for is unknown. But of course, it can’t continue forever and ultimately the conversion of too much hydrogen would bring a halt to the radiation process; unless the conversion products were also superconductive.
Benefits of this model
In summary then, this superconducting model neatly accounts for a number of observations about the Sun:
Its average density
Its magnetic fields
Its (seemingly unlimited) power supply
Its minimum size
The solar wind
The darkness of sunspots
Conclusion
It’s possible that our Sun (and many stars) consists primarily of hydrogen that is first compressed into a solid, then further compressed to the point where the atoms are almost unable to vibrate. At this point the solid becomes ‘frozen’ at near-zero absolute temperature. This allows the substance to become superconducting and large electrical currents to circle within it.
These currents produce magnetic fields and focus themselves into a mid-region within the Sun, leaving a net positive area near its surface. This positive area then electrically discharges into the surface atmosphere, producing light, heat, solar wind, and occasional flares.
—————–
[1] Although the evidence is sketchy because the craft was not designed to measure that.
http://www.thunderbolts.info/tpod/2010/arch10/100204ulysses.htm
[2] Astronomers speculate that the interior of Jupiter and Saturn consists of metallic hydrogen. Assuming their calculations are correct, if metallic hydrogen can form within a gas-ball the size of Jupiter, there should be no problem in it doing likewise within the Sun.
http://alternativephysics.org/
Web Caffè Bookique [Facebook]
A Superconducting Model
of the Sun
by Bernard Burchell
There are two popular and competing models that describe how the Sun works. As in, how it glows, gives off heat, light, solar wind, etc.
The most well-known of these is the thermonuclear model.
In this model, loose accumulations of interstellar hydrogen are drawn together under the pull of their own gravity and into a sphere of compressing gas. The process involves friction, which causes the gas to glow either red or infrared, and leads to what we call a brown dwarf.
If this process were allowed to continue, and with increasingly larger amounts of hydrogen involved, the pressure at the interior of the ball would become so high that the hydrogen would undergo nuclear fusion: first into helium, and then into higher order elements. The energy released by this fusion process would cause the gaseous ball to glow white-hot, leading to a star like our Sun.
In the thermonuclear model the Sun’s interior is millions of degrees Celsius. This steadily decreases toward the surface where we observe a temperature of around five thousand degrees.
A lesser-known explanation is the electric model.
In this model, the glow we observe from the Sun’s surface is not caused by fusion but by electrical discharges; similar to the electric arcs/sparks seen on a welding device. For this to happen the Sun must have a strong net-positive charge. It is made out of plasma (ionised gas) and this positive plasma steadily discharges at its surface. Its interior is a few thousand degrees throughout; slightly cooler than the photosphere surface. And its interior charge counteracts gravity to prevent further collapse.
(The above is a very brief introduction and admittedly the subject takes some getting used to. For a better description of the Electric Sun model see
http://www.electric-cosmos.org/sun.htm )
http://www.youtube.com/playlist?list=PLwOAYhBuU3Ufr53AnJv9RLousgVN4G_uX
Of these two models, the more likely is the electrical one. It correctly accounts for the magnetic fields, the appearance of tufts, its temperature increase whilst heading outward toward the corona, the solar wind, and occasional flaring.

In these close-ups of sunspots we see twisted glowing strands. These are consistent with Birkeland currents, a type of electrical arcing seen in plasma discharges. Credit: SST, Royal Swedish Acadmey of Sciences

Here we see coronial plasma loops, an effect related to magnetism. The Sun’s magnetic field can also be detected far out into the solar system. Credit: M. Aschwanden et al. (LMSAL), TRACE, NASA

This diagram shows the Sun as a large positively charged ball and the voltage potential arising from it. The high positive charge causes a discharge of protons into the photospheric gasses, leading to plasma glowing effects. The protons then continue to accelerate and strike the corona (an outer layer of gas surrounding the Sun) at high speed, leading to even higher temperatures there. Credit: The Electric Universe, Thornhill & Talbott
Where’s the power?
Despite its success though, the electric Sun model does appear to suffer a major deficiency. Namely the question: what powers this electrical giant? Specifically, what gives it a positive charge, and what drives the currents necessary to explain its magnetic fields?
According to the theory, the Sun is powered by streams of electrons funnelling inward toward the polar regions. These ‘galactic powerlines’ interconnect all the stars in the galaxy and feed them the necessary current to power their photospheres. The presence of these has been partially observed via the Ulysses craft, which passed over the polar regions [1].
But while there could be little disagreement that a positively-charged ball would attract electrons, there are major problems in suggesting that this could be its power source.
First, a stream of electrons ‘falling’ into the Sun is not going to do much other than steadily discharge it. In order to power an electrical device (e.g. a desk lamp), charge must be forcefully fed into it and then extracted again. This is because the device has resistance that needs to be overcome. But the electrical Sun model describes a one-way inward current flow. And it’s not forced, just free-falling.
Second, since the Sun is emitting positive charges, the net current supply must consist of protons rather than electrons otherwise the output current – the solar wind – would eventually cease. This is a big problem because protons won’t move toward a net-positive charge unless they are somehow forced or initially fired (from where?) at high speeds. But the model allows for no such inward positive flow and no observations support it.
So what then could explain the power supply and nature of the Sun?
What if…?
What if, instead of the high-temperature thermonuclear model, we said the Sun steadily grew cooler as we headed inwards? And by ‘cooler’, I don’t just mean in a sense relative to its surface, as in a few thousand degrees. Nor even a few hundred degrees. And not even a few degrees below room temperature, but colder again.
What if the temperatures in the Sun’s interior became so cold that they approached levels nearing absolute zero Kelvin – the lowest temperature possible for any material?
The idea sounds absurd! It is the complete opposite of the conventional model, with its millions-of-degrees thermonuclear core. And after all,how could a compressed gas become cold?
Extreme compression of a gas
To understand how this might be possible, consider an airtight cylinder with a piston at one end. We fill the cylinder with nitrogen (which is basically air minus oxygen) and begin to apply pressure to the piston. What will happen?
This is somewhat like compressing air inside a bicycle pump. The pressure will increase and the temperature will rise. After a while though, this heat from the compression process will dissipate and the temperature will return to the surrounding air temperature.
So we push the piston further. Once again, the nitrogen pressure will increase and the temperature will temporarily rise before returning to normal.
Now let’s suppose our cylinder was very strong and we were able to apply a very high amount of force to the piston. In this case the gas will compress so much that it will cease being a gas and become a liquid: liquid nitrogen.
Take this idea further. We continue to apply ever larger forces on the piston. Eventually this liquid will be forced to collapse into ‘solidnitrogen’.
As is well known, liquid and solid nitrogen are very cold substances. However it needs to be quickly pointed out that we have not made anything cold. Rather, the liquid and solid states of nitrogen will at first be at high temperature and pressure. After a while, the heat will dissipate and temperature will return to the surrounding air temperature. But compared to regular (cold) liquid or solid nitrogen, the pressure is very high and the substance would explode into gas if released.
Compression under gravity
Now consider a similar situation for a star. Under the standard astronomy model, stars are formed when loose accumulations of hydrogen gas are drawn together under the force of their own gravity. As this occurs, gas is compressed and heats up, giving out infrared heat. This increase in temperature might halt the compression process for a time. But adding more gas will force the compression to continue.
Eventually the internal gaseous resistance will give way, allowing the hydrogen to liquefy. Although this liquid will be still be quite hot. We continue to add more hydrogen, increasing the external pressure. Eventually this liquid also gives way, and the hydrogen collapses into a solid.
At this stage the solid is somewhat disorganised, its atoms not arranged according to any particular pattern. We continue to increase pressure. Eventually the hydrogen atoms are forced into crystalline lattice structures. We could now refer to this as ‘metallic hydrogen’.
The atoms have now become rather restricted in their movement. They are unable to move about freely as they did in their gas, liquid or semi-solid state. Instead they are restricted into vibrating along short distances.
Despite the restriction in distance though, this rapid movement still accounts for a high temperature; since that vibration is essentially the definition of temperature. But if enough pressure were applied to the lattice, the hydrogen atoms would be almost unable to move. They would effectively have become frozen and could thus be described as having a temperature of near absolute zero.
So… what happens when we freeze a metal or crystalline material to near absolute zero? The title of this essay gives it away: it becomes superconducting!
As is known, superconductors allow electrons to flow through them without resistance. A superconductor formed into a ring or disk can maintain an internal electric current that circles forever. And as it does so, it emits a magnetic field, just as an electromagnetic coil would do. Except a superconductor magnet requires no power supply to maintain it.
Therefore a superconductor formed into a ball should also be able to maintain internal currents that cycled forever and without the need for any power supply.

Electrons circling within a superconducting ball or disk.
Current cross-section of a wire
So what does this mean? Quite obviously, if the Sun were a giant superconductor, we should likewise expect it to contain powerful circling currents. These currents would then generate large magnetic fields. And we certainly do observe magnetic fields and related effects like plasma loops coming from the Sun (see eariler diagram).
But there is more to this story than just magnetism.
Consider now two parallel wires, each carrying a current in the same direction. We know from observation that these will attract each other.

Magnetic attraction from parallel currents.
Now consider the situation inside just a single current-carrying wire. We will give this wire a rectangular cross section, with width is twice its depth. Below is an enlarged top and cross-section view.

Electrons stationary inside a wire with rectangular cross-section.
Here we see the wire with protons and electrons both stationary, i.e. no current is flowing yet. If we draw an imaginary dividing line down the middle of the wire we notice that it would become analogous to the two parallel current-carrying wires described earlier, except without a gap between them. Therefore, like the two-wire situation, we should expect flowing electron streams to attract each other like so:

Electrons flowing inside a wire with rectangular cross-section.
Here we see an electron current flowing and the electrons are now concentrated along the middle of the wire. This gives the inner part of the wire a slight negative charge. Meanwhile the outer edges of the wire have a lack of electrons and therefore gain a slight positive charge.
Does this happen in reality? It doesn’t. Experiments show that current density remains uniform when DC currents are involved. And when an AC current is fed through, the electrons push themselves against the walls of a wire. This is called the ‘skin effect’.
Given our knowledge of magnetism however, this appears curious. Because by all accounts the electrons should accumulate into the middle portion of the wire in both the DC and AC scenarios.
It appears something else is going on inside wires, namely ‘eddy currents’. These are tiny ‘whirlpool’ currents that appear to develop inside conductors, repelling attractive current flow and pushing the electrons to the outside. In the AC case the effect is more pronounced.
But we are not dealing with regular conductors. We are dealing with superconductors, and these have rather different properties where magnetism is concerned. Given that superconductors have zero resistance, perhaps eddy currents don’t develop or are too minor to be a problem. Therefore for superconducting wire, especially where large currents are concerned, magnetic forces may well focus the electrons along the middle of the wire, as indicated above.
Next consider the situation for a superconducting disk. We’ll start by having electrons circle around its centre.

Electrons circling in disk (no magnetic attraction).
Since these electrons are moving in parallel, we should expect them to magnetically attract each other, resulting in a situation like this:

Electrons circling in disk, with internal magnetic attraction.
As with the rectangular wire above, the electrons have concentrated themselves into a negatively charged ring-shaped region located between the centre and the perimeter. The reason for a ring and not a small inner disk is that the electrons moving in opposite directions on either side of the ‘inner disk’ will magnetically repel each other. The result will be a negatively charged ring with a positively charged regions either side: one in the centre and the other along the outer part of the disk, as shown below.

(Fig 10) Magnetic attraction and repulsion of circling electrons leaves positive and negative regions within a disk.
Now extend the above situation to a ball-shaped superconductor. Particularly one the size of the Sun. We should expect large internal currents, which focus themselves into a middle negative region, whilst leaving a positive region in the centre and on the outside.
This outer positive region is of particular interest. If the charge were strong enough, we should expect electrical discharges to occur across the surface of the Sun, as protons leapt off the surface.
If the surface were covered by a gaseous layer (and it is with the Sun) the motion of protons passing through it would cause the surface to light up with electrical sparks, also known as ‘anode tufts’. We should also expect a steady discharge of protons accelerating out as a solar wind. And if for some reason the sparking stopped at some area, causing sunspots, we should also expect those regions to be darker because we would now be looking at the relatively cooler solid surface of the Sun. And sure enough, this all corresponds to what we see!
Since currents can circle forever within a superconductor, the above describes a model in which a star can glow indefinitely, without any external power source or requirement for internal fusion. Electrons will still be attracted and flow inward toward the Sun’s positive surface. However, these are not required for the Sun to glow and act more as a power discharge than a power supply.
What about density?
In order for this model to be viable it needs to show an agreeable density. The density of the Sun is 1400kg/m3 or 1.4 times that of water. This is of course an average. We should expect the density to be less near the surface and steadily increase toward a value higher at the centre.
So how does the 1400 number fit with this model?
Below is a table showing the densities of various substances in ascending order and compared with the Sun’s average.
Substance Density (kg/m3)
Hydrogen gas 0.09
Helium gas 0.18
Helium solid 0.21
Nitrogen gas 1.3
Tungsten Hexafluoride gas 13
Hydrogen liquid 71
Helium liquid 125
Lithium solid 534
Hydrogen solid 600
Nitrogen liquid 807
Water liquid 1000
Nitrogen solid 1030
Sun (average) 1400
Quartz (SiO2 – typical rock) 2600
Diamond (carbon) 3500
Iron 7900
Lead 11000
Note the position of hydrogen gas on the list. At 0.09 kg/m3, it is far less than the 1400 required. Likewise with heavier gasses such as helium and nitrogen. In fact even the densest gas known, tungsten hexafluoride, falls well short of what is required. This would appear to rule out an interior of a gaseous or plasma nature.
Hydrogen in its liquid state is still too light, as is helium. Liquids made of heavier elements would certainly work, although that requires them to be far above hydrogen on the periodic table, and which requires going back to the problematic fusion model.
Going to typical solids, such as diamond (compressed carbon) places us too high on the list. Carbon is said to be a common fusion by-product in the thermonuclear model.
But solid hydrogen appears nearer the mark.
Solid hydrogen has a density of 600kg/m3. The 1400 Sun-density value seems to correspond to hydrogen compressed to a bit over double that amount. If we estimate a higher density for the Sun’s interior of 1800kg/m3, that makes it 3 times the 600 hydrogen figure. Admittedly the 1800 number is a guess and the real density might be higher; although could not be too much higher because the 1400 average would be wrong.
Thus, a Sun comprised of compressed solidified hydrogen would have a density consistent with what we observe, and is supportive of the model described here.
Of course it would also be possible to achieve the 1400 average using a combination of elements. Metallic lithium for example has a density of 534kg/m3. So compressing that several times can give the necessary density. Or combining it with heavier elements like iron would also work. However, it will require fusion and also require the relative abundance of such substances be very different than what is observed in the universe. Thus metallic hydrogen still seems the more likely candidate [2].
Solar Oblateness and Rotation
Here’s another point to consider. As we know, the Sun rotates on its axis, and this rotation gives rise to a bulge around its equator, similar to the way the Earth bulges around its equator.
The degree of bulge – called the solar oblateness – however, is far smaller than what would be expected for a flexible rotating ball of that size, mass and angular speed. In fact the Sun comes close to being a perfect sphere.
But if the interior of the Sun were not made of gas or plasma, and was instead a solid ball, the above observations on oblateness would make sense. Because only the outer flexible layer of the photosphere gasses would be able to bulge and the amount of bulge would be limited by its thickness.
And speaking of rotation, another interesting fact is that the Sun rotates faster at its equator than at its poles. This tells us that some of the observed rotation may just be a surface effect and leads to the possibility that the interior may be rotating even slower again. In fact for all we know, the interior may not rotate at all and the surface rotation we observe may be caused by interior electrical currents pushing the photosphere around. If this were the case it would explain why the interior solid region formed as a sphere rather than an ‘ellipsoid’.
The overall current flow
Let’s now look at the overall current flow. The above diagram (Fig 10) showing positive and negative regions within a disk won’t work for a sphere. Namely, it won’t be possible for currents to circle a sphere in all directions because electrons moving head-on would magnetically repel. Therefore, it will instead be necessary for currents to largely flow in the same direction.
In the previous section it was speculated that the Sun’s apparent rotation only represented the flow of its photosphere, and that this was being caused by the electron currents flowing in the solid interior.
This does seem likely. Since the gasses within the photosphere are ionized into a plasma, the protons within the plasma would be magnetically attracted to the circling electrons and dragged across the solid surface underneath. Meanwhile the electrons in the photosphere will move along with the protons, giving an overall movement of the photosphere surface.
This motion of the photosphere suggests an interior current flow in layers, i.e. many current loops running parallel to the Sun’s equator. The overall current flow and resulting charged regions will then look something like this:

(Fig 11) Electron currents cycle eastwards along the equator and in many layers parallel to it. This leaves positive and negative regions within. Arrows represent direction of electron flow and the vertical grey line is an “axis” of rotation.
As with the disk, this results in positive and negative regions within. What happens at the polar regions is uncertain since we won’t be able to fit in a ‘mini disk’ there. So here they are speculatively shown as having the adjacent positive regions spill over onto them. As a result we end up with a sphere covered by an outer positive layer.
Magnetic repulsion of the surface
Next we’ll look at the interaction between the moving photosphere and stationary interior.
In this model, protons within the solid interior remain stationary while the electrons cycle west-to-east, and the photosphere moves in the same direction, albeit more slowly.
Since the protons in the photosphere are moving against those in the interior, they will magnetically repel and be pushed away. Meanwhile the electrons in the photosphere will be magnetically attracted. This diagram shows the resulting force directions.

(Fig 12) Magnetic attraction/repulsion between photosphere and interior (top view, looking down on north pole). Protons experience repulsion and electrons attraction as they both move over the net-positive surface of the interior.
This interaction turns out to be very important. We know from Coulomb’s law that a sphere containing equal amounts of positive and negative charge can have zero net-attraction. This will be the case when the charge is distributed with radial symmetry, i.e. if the charge is arranged into positive and negative spherical shells. The charge distribution diagram above (Fig 11) shows something close to this situation.
But if differently charged regions of the interior and exterior regions were moving against each other (as indicated in Fig 12), this can lead to a net repulsion of the photosphere’s protons, resulting in a glow-discharge and solar winds.
In fact without the photosphere’s rotation, it might be that the Sun wouldn’t glow at all. It might also be true that sunspots are caused by a slowing down of photosphere motion (for unknown reasons), and hence a halting of the discharge process at those places.
No miniature stars
The electric star model discussed at the opening of this essay is part of a broader body of knowledge and theory known as the Electric Universe (EU) model. One of the big benefits of the EU model is that it is able to recreate observed astronomical phenomena in a laboratory. For example it is possible to produce phenomena that look strikingly similar to nebulae formations inside plasma focus devices.
The fact that we can do this is very impressive and tells us EU theory must be on the right track in much of what it describes.
Despite this validity however, no similar success has been achieved in creating a small-scale star in a laboratory. The same is true throughout the universe: no miniature stars are seen floating about our galaxy or elsewhere. It appears that white stars must be of a minimum size or they won’t function.
This should be a big clue that there is more than just electricity at play in creating a star. Namely, that a large amount of gravity is required in order for a star to advance beyond the brown dwarf stage and become a white star. This point further supports the compressed superconducting model.
How long can it last?
Can the Sun/star model described here radiate forever? On the face of it it would appear so. Superconductors can maintain a current continuously without decrease. Therefore it would seem that stars could output an unlimited supply of energy.
Problem is, our Sun also outputs solar wind and flares – amounting to a million tons of matter every second and consisting mainly of protons. This process clearly can’t continue forever. At some point it must come to a stop when the Sun runs out of ejectable protons or becomes too negatively charged (as a result of losing protons) and is unable to eject more. At this point the electrical discharges in the photosphere would cease and the Sun would become dark.
Another consideration is the inflow of electrons. As discussed earlier, a positive charged surface would be expected to attract a steady stream of electrons. Initially these electrons might add to the those already circling within the interior. This would increase the current flows, the magnetic fields, and the brightness/intensity of the solar output. Eventually though, the increase in negative charge would be enough to halt the output of protons, again leading to the Sun’s demise.
Fusion
Something also needs to be said about the conversion of hydrogen into heavier elements, i.e. fusion. The electric star model forbids fusion within the Sun’s interior but allows for it to take place within the electrical discharge area of the photosphere.
In this superconductor model we’ll allow that the same should apply. Namely that there should be no fusion activity within the frozen interior but that fusion will take place either in the photosphere or just beneath it. How long this can continue for is unknown. But of course, it can’t continue forever and ultimately the conversion of too much hydrogen would bring a halt to the radiation process; unless the conversion products were also superconductive.
Benefits of this model
In summary then, this superconducting model neatly accounts for a number of observations about the Sun:
Its average density
Its magnetic fields
Its (seemingly unlimited) power supply
Its minimum size
The solar wind
The darkness of sunspots
Conclusion
It’s possible that our Sun (and many stars) consists primarily of hydrogen that is first compressed into a solid, then further compressed to the point where the atoms are almost unable to vibrate. At this point the solid becomes ‘frozen’ at near-zero absolute temperature. This allows the substance to become superconducting and large electrical currents to circle within it.
These currents produce magnetic fields and focus themselves into a mid-region within the Sun, leaving a net positive area near its surface. This positive area then electrically discharges into the surface atmosphere, producing light, heat, solar wind, and occasional flares.
—————–
[1] Although the evidence is sketchy because the craft was not designed to measure that.
http://www.thunderbolts.info/tpod/2010/arch10/100204ulysses.htm
[2] Astronomers speculate that the interior of Jupiter and Saturn consists of metallic hydrogen. Assuming their calculations are correct, if metallic hydrogen can form within a gas-ball the size of Jupiter, there should be no problem in it doing likewise within the Sun.
http://alternativephysics.org/

Nessun commento:
Posta un commento